Today is World Tessellation day. So what is a tessellation anyway? Tessellation is just a fancy word for a tiling pattern. Mathematically this means covering a flat surface using one or more geometric shapes with no overlaps and no gaps.






Regular tilings are all around us. We can see them in paving blocks,honeycombs, chainlink fences.


To study tilings mathematicians study their symmetries. A symmetry is any transformation that leaves the pattern unchanged. Let us consider the square tiling for instance. Imagine it lying on the X-Y plane. Now let us see what happens when we move all points in the X-direction by 1 unit.
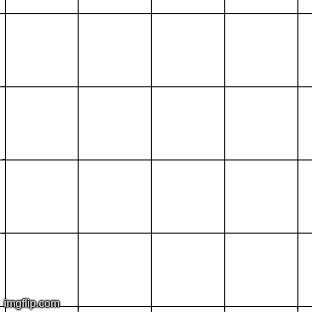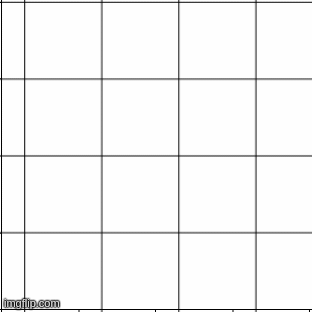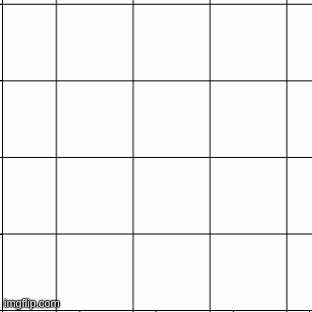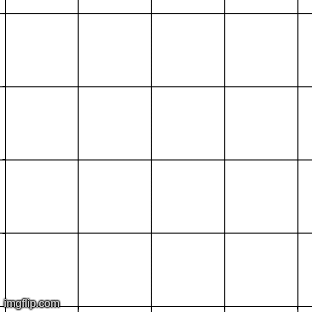
The horizontal lines i.e. the lines of the type stay where they are. The line
goes to the line
. The line
goes to the line
and so on. So overall the points on the grid go to other points on the grid. Thus
is a transformation that leaves the pattern unchanged. Thus it is a symmetry of the tessellation. It is easy to see that the transformation
is also a symmetry.What other symmetries can you think of? Applying one symmetry after another is also a symmetry! Thus if we denote the above two symmetries as
and
then
(first apply
then
) is also a symmetry. In fact the set of all symmetries form a group. All transformations of the type
(apply A n times then B m times) for some integers
and
are also symmetries. But those do not constitute all symmetries. We leave it to the reader to find more. (Hint: reflections). Other tilings also contain rotational symmetries like the one given below. A rotation by
leaves the pattern unchanged.
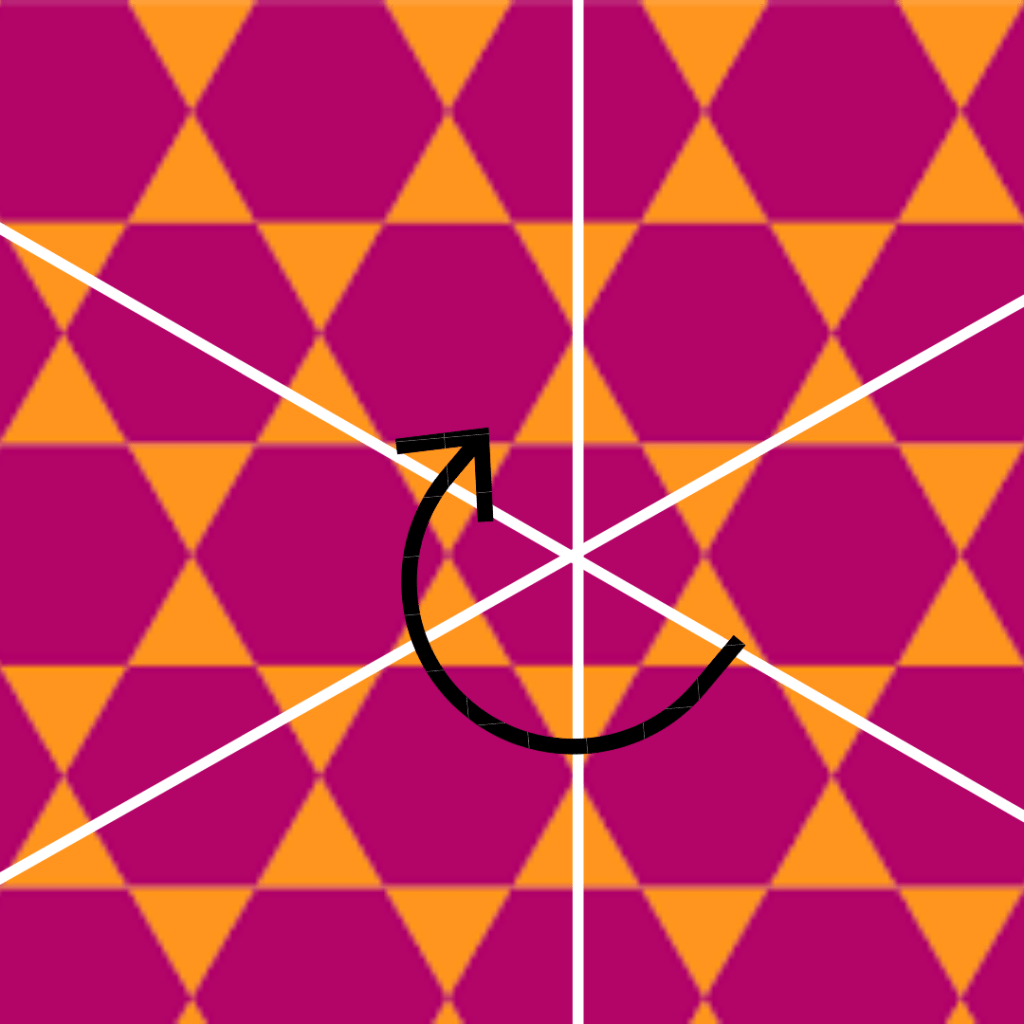
The groups that arise as symmetry groups of tessellations are aptly named wallpaper groups. The surprising fact is that there are only 17 such groups that give rise to such myriad tilings!
Until now we have only seen tilings with a fixed pattern repeated indefinitely by translating it. But there exist tilings that are not of this form.

Another interesting example is the chair tiling.
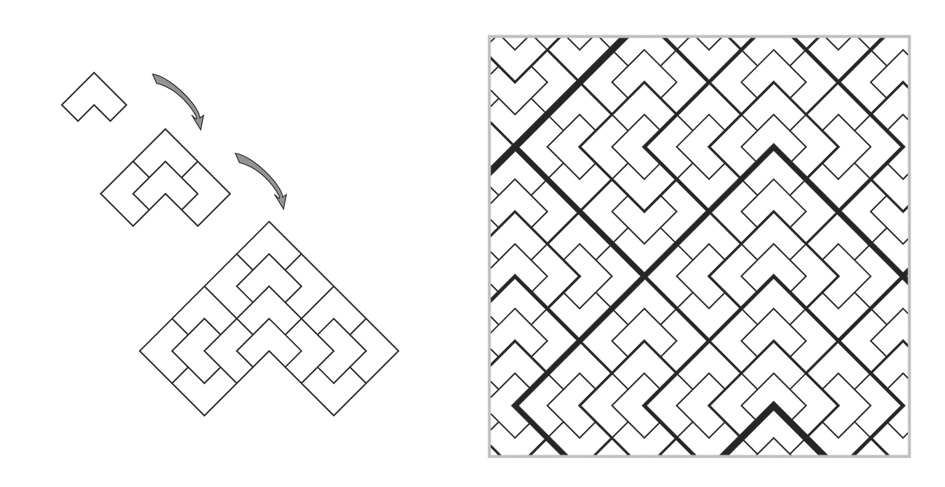
It is formed by an iterative process in which you take four copies of the previous iteration and fit them together to form an L-shaped tile.
Further reading:
For a classification of the wallpaper groups see here .
Reblogged this on REFLECTIONS and commented:
My post on Science Defined
LikeLike
Didn’t realize it was world tesselation day! These are so fun to look at! Than you for sharing. 🙂
https://mathsux.org/
LikeLike